At Semantic Arts we often come across ontologies whose developers seem to take pride in the number of classes they have created, giving the impression that more classes equate to a better ontology. We disagree with this perspective and as evidence, point to Occam’s Razor, a problem-solving principle that states, “Entities should not be multiplied without necessity.” More is not always better. This post introduces Facet Math and demonstrates how to contain runaway class creation during ontology design.
Semantic technology is suited to making complex information intellectually manageable and huge class counts are counterproductive. Enterprise data management is complex enough without making the problem worse. Adding unnecessary classes can render enterprise data management intellectually unmanageable. Fortunately, the solution comes in the form of a simple modeling change.
Facet Math leverages core concepts and pushes fine-grained distinction to the edges of the data model. This reduces class counts and complexity without losing any informational fidelity. Here is a scenario that demonstrates spurious class creation in the literature domain. Since literature can be sliced many ways, it is easy to justify building in complexity as data structures are designed. This example demonstrates a typical approach and then pivots to a more elegant Facet Math solution.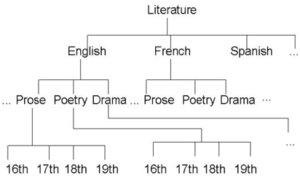
A taxonomy is a natural choice for the literature domain. To get to each leaf, the whole path must be modeled adding a multiplier with each additional level in the taxonomy. This case shows the multiplicative effect and would result in a tree with 1000 leaves (10*10*10) assuming it had:
10 languages
10 genres
10 time periods
Taxonomies typically are not that regular though they do chart a path from the topmost concept down to each leaf. Modelers tend to model the whole path which multiplies the result set. Having to navigate taxonomy paths makes working with the information more difficult. The path must be disassembled to work with the components it has aggregated.
This temptation to model taxonomy paths into classes and/or class hierarchies creates a great deal of complexity. The languages, genres, and time periods in the example are really literature categories. This is where Facet Math kicks in taking an additive approach by designing them as distinct categories. Using those categories for faceted search and dataset assembly returns all the required data. Here is how it works.
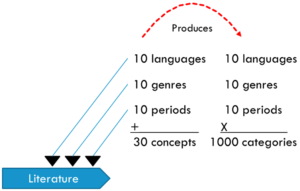
To apply Facet Math, remove the category duplication from the original taxonomy by refactoring them as category facets. The facets enable exactly the same data representation:
10 languages
10 genres
10 time periods
By applying Facet Math principles, the concept count is reduced by two orders of magnitude. Where the paths multiplied to produce 1000 concepts, facets are only added and there are now only 30. This results in two orders of magnitude reduction!
Sure, this is a simple example. Looking at a published ontology might be more enlightening.
SNOMED (Systematized Nomenclature of Medicine—Clinical Terms) ontology is a real-world example.
Since the thesis here is looking at fat reduction, here is the class hierarchy in SNOMED to get from the top most class to Gastric Bypass.
Notice that Procedure appears in four levels, Anastomosis and Stomach each appear in two levels. This hierarchy is a path containing paths.
SNOMED’s maximum class hierarchy depth is twenty-seven. Given the multiplicative effect shown above in the first example, SNOMED having 357,533 classes, while disappointing, is not surprising. The medical domain is highly complex but applying Facet Math to SNOMED would surely generate some serious weight reduction. We know this is possible because we have done it with clients. In one case Semantic Arts produced a reduction from over one hundred fifty thousand concepts to several hundred without any loss in data fidelity.
Bloated ontologies contain far more complexity than is necessary. Humans cannot possibly memorize a hundred thousand concepts, but several hundred are intellectually manageable. Computers also benefit from reduced class counts. Machine Learning and Artificial Intelligence applications have fewer, more focused concepts to work with so they can move through large datasets more quickly and effectively.
It is time to apply Occam’s Razor and avoid creating unnecessary classes. It is time to design ontologies using Facet Math.
