Phil Blackwood

This blog post is for anyone responsible for Enterprise data management who would like to save time and costs by re-using a great piece of modeling work. It updates an earlier blog post, “A brief introduction to the gist semantic model”.

A core semantic model, also called an upper ontology, is a common model across the Enterprise that includes major concepts such as Event, Agreement, and Organization. Using an upper ontology greatly simplifies data integration across the Enterprise. Imagine, for example, being able to see all financial Events across your Enterprise; that kind of visibility would be a powerful enabler for accurate financial tracking, planning, and reporting.

If you are ready to incorporate semantics into your data environment, consider using the gist upper ontology. gist is available for free from Semantic Arts under a creative commons license. It is based on more than a hundred data-centric projects done with major corporations in a variety of lines of business.  gist “is designed to have the maximum coverage of typical business ontology concepts with the fewest number of primitives and the least amount of ambiguity.”  The Wikipedia entry for upper ontologies compares gist to other ontologies and gives a good sense of why gist is a match for Enterprise data management: it is comprehensive, unambiguous, and easy to understand.

 

So, what exactly is in gist?

First, gist includes types of things (classes) involved in running an Enterprise. Some of the more frequently used gist classes, grouped for ease of understanding, are:

Some of these classes have subclasses that are not shown. For example, an Intention could be a Goal or a Requirement.

Gist also includes properties that are used to describe things and to describe relationships between things. Many of the gist properties can be approximately grouped as above:

Other commonly used gist properties include:

Next, let’s look at a few typical graph patterns that illustrate how classes and properties work together to model the Enterprise world.

An Account might look like:

An Event might look like:

An ID such as a driver’s license might look like:

To explore gist in more detail, you can view it in an ontology editor such as Protégé. Try looking up the Classes and Properties in each group above (who, what, where, why, etc.). Join the gist Forum (select and scroll to the bottom) for regular discussion and updates.

Take a look at gist.  It’s worth your time, because adopting gist as your upper ontology can be a significant step toward reversing the proliferation of data siloes within your Enterprise.

Further reading and videos:

3-part video introduction to gist:

1. https://www.youtube.com/watch?v=YbaDZSuhm54&t=123s
2. https://www.youtube.com/watch?v=UzNVIErpGpQ&t=206s
3. https://www.youtube.com/watch?v=2g0E6cFro18&t=14s

Software Wasteland, by Dave McComb

The Data-Centric Revolution, by Dave McComb

Demystifying OWL for the Enterprise, by Michael Uschold

 

Diagrams in this blog post were generated using a visualization tool.

This blog post is for anyone interested in mathematics and knowledge representation as associated with career progression in today’s changing information eco-system. Mathematics and knowledge representation have a strong common thread; they both require finding good abstractions and simple, elegant solutions, and they both have a foundation in set theory. It could be used as the starting point for an accessible academic research project that deals with the foundation of mathematics and will also develop commercially marketable knowledge representation skills.

Hypothesis: Could the vast body of mathematical knowledge be put into a knowledge graph? Let’s explore, because doing so could provide a searchable data base of mathematical concepts and help identify previously unrecognized connections between concepts.

Every piece of data in a knowledge graph is a semantic triple of the form:

subject – predicate – object.

A brief look through mathematical documentation reveals the frequent appearance of semantic triples of the form:

A implies B, where A and B are statements.

“A implies B” is itself a statement, equivalent to “If A then B”. Definitions, axioms, and theorems can be stated using these if/then statements. The if/then statements build on each other, starting with a foundation of definitions and axioms (statements so fundamental they are made without proof). Furthermore, the predicate “implies” is transitive, meaning an “implies” relationship can be inferred from a chain of other “implies” relationships.

…. hence the possibility of programmatically discovering relationships between statements.

Before speculating further, let’s examine two examples from the field of point set topology, which deals abstractly with concepts like continuity, connectedness, and compactness.

Definition: a collection of sets T is a topology if and only if the following are true:

• the union of sets in any subcollection of T is a member of T
• the intersection of sets in any finite subcollection of T is a member of T.

Problem: Suppose there is a topology T and a set X that satisfies the following condition:

• for every member x of X there is a set Tx in T with x in Tx and Tx a subset of X.

Show that X is a member of T.

Here’s a diagram showing the condition stated in the problem, which holds for every x in X:

Perhaps you can already see what happens if we take the union of all of the Tx’s, one for each x in X.

In English, the solution to the problem is:

The union of all sets Tx is a subset of X because every Tx is a subset of X.

The union of all sets Tx contains X because there is a Tx containing x, for every x in X.

Based on the two statements above, the union of all sets Tx equals X because it is both a subset and a superset of X.

Finally, since every Tx belongs to T, the union of all sets Tx (which is X) is a member of T.

Let’s see how some of this might look in a knowledge graph. According to the definition of topology:

Applying this pattern to the problem above, we find:

While it may seem simple to recognize the sameness of the patterns on the left side of the two diagrams above, what precisely is it that makes the pattern in the problem match the pattern in the definition of topology? The definition applies because both left-hand statements conform to the same graph pattern:

This graph pattern consists of two triple patterns, each of which has the form:

[class of the subject] – predicate – [class or datatype of the object].

We now have the beginnings of a formal ontology based on triple patterns that we have encountered so far. Statements, including complex ones, can be represented using triples.

Note: in the Web Ontology Language, the properties hasSubject, hasPredicate, and hasObject will need to be annotation properties (they can be used in queries but will not be part of automated inference).

Major concepts can be represented as classes:

It’s generally good practice to use classes for major concepts, while using other methods such as categories to model other distinctions needed.

Other triple patterns we have seen describe a variety of relationships between sets and collections of sets, summarized as:

Could the vast body of mathematical knowledge be put into a knowledge graph? Certainly, a substantial amount of it, that which can be expressed as “A implies B”.

However, much remains to be done. For example, we have not looked at how to distinguish between a statement that is asserted to be true versus, for example, a statement that is part of an “if” clause.

Or imagine a math teacher on Monday saying “x + 3 = 7” and on Tuesday saying “x – 8 = 4”. In a knowledge graph, every thing has a unique permanent ID, so if x is 4 on Monday, it is still 4 on Tuesday. Perhaps there is a simple way to bridge the typical mathematical re-use of non-specific names like “x” and the knowledge graph requirement of unique IDs; finding it is left to the reader.

For a good challenge, try stating the Urysohn Lemma using triples, and see how much of its proof can be represented as triples and triple patterns.

To understand modeling options within the Web Ontology Language (OWL), I refer the reader to the book Demystifying OWL for the Enterprise by Michael Uschold. The serious investigator might also want to explore the semantics of rdf* since it explicitly deals with the semantics of statements.

Special thanks to Irina Filitovich for her insights and comments.

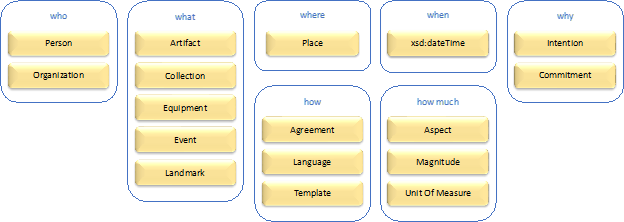
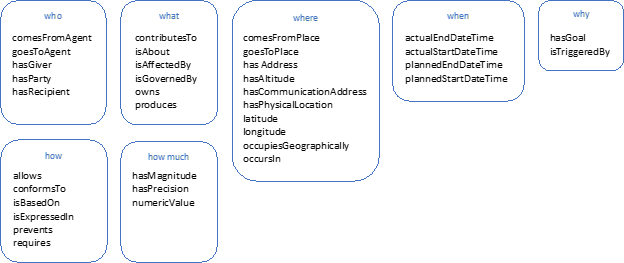
This blog post is for anyone interested in understanding units of measure for the physical world.

The dominant standard for units of measure is the International System of Units, part of a collaborative effort that describes itself as:

Working together to promote and advance the global comparability of measurements.

While the International System of Units is defined in a document, QUDT has taken the next step and defined an ontology and a set of reference data that can be queried via a public SPARQL endpoint. QUDT provides a wonderful resource for data-centric efforts that involve quantitative data.

QUDT is an acronym for Quantities, Units, Dimensions, and Types. With 72 classes and 178 properties in its ontology, QUDT may at first appear daunting. In this note, we will use a few simple SPARQL queries to explore the QUDT graph. The main questions we will answer are:

1. What units are applicable for a given measurable characteristic?
2. How do I convert a value from one unit to another?
3. How does QUDT support dimensional analysis?
4. How can units be defined in terms of the International System of Units?

Let’s jump right in. Please follow along as a hands-on exercise. Pull up the QUDT web site at:

https://qudt.org/

On the right side of the QUDT home page select the link to the QUDT SPARQL Endpoint where we can run queries:

From the SPARQL endpoint, select the query option.

Question 1: What units are applicable for a given measurable characteristic?

First, let’s at the measurable characteristics defined in QUDT. Copy-paste this query into the SPARQL endpoint:

prefix qudt: <http://qudt.org/schema/qudt/>

prefix rdf:  <http://www.w3.org/1999/02/22-rdf-syntax-ns#>

prefix rdfs: <http://www.w3.org/2000/01/rdf-schema#>

prefix owl:  <http://www.w3.org/2002/07/owl#>

prefix xsd:  <http://www.w3.org/2001/XMLSchema#>

select ?qk

where {?qk rdf:type qudt:QuantityKind . }

order by ?qk

 

QUDT calls the measurable characteristics QuantityKinds.

Note that there is a Filter box that lets us search the output.

Type “acceleration” into the Filter box and then select the first value, Acceleration, to get a new tab showing the properties of Acceleration. Voila, we get a list of units for measuring acceleration:

Now to get a complete answer to our first question, just add a line to the query:

prefix qudt: <http://qudt.org/schema/qudt/>

prefix rdf:  <http://www.w3.org/1999/02/22-rdf-syntax-ns#>

prefix rdfs: <http://www.w3.org/2000/01/rdf-schema#>

prefix owl:  <http://www.w3.org/2002/07/owl#>

prefix xsd:  <http://www.w3.org/2001/XMLSchema#>

select ?qk ?unit

where {

?qk rdf:type qudt:QuantityKind ;

qudt:applicableUnit ?unit  ; # new line

.

}

order by ?qk ?unit

The output shows the units of measure for each QuantityKind.

Question 2: How do I convert a value from one unit to another?

Next, let’s look at how to do a unit conversion from feet to yards, with meter as an intermediary:

To convert from feet to meters, multiply by 0.3048. Then to convert from meters to yards, divide by 0.9144. Therefore, to convert from feet to yards, first multiply by 0.3048 and then divide by 0.9144. For example:

27 feet = 27 x (0.3048/0.9144) yards

= 9 yards

The 0.3048 and 0.9144 are in QUDT as the conversionMultipliers of foot and yard, respectively. You can see them with this query:

prefix qudt: <http://qudt.org/schema/qudt/>

prefix rdf:  <http://www.w3.org/1999/02/22-rdf-syntax-ns#>

prefix rdfs: <http://www.w3.org/2000/01/rdf-schema#>

prefix owl:  <http://www.w3.org/2002/07/owl#>

prefix xsd:  <http://www.w3.org/2001/XMLSchema#>

select ?unit ?multiplier

where {

values ?unit {

<http://qudt.org/vocab/unit/FT>

<http://qudt.org/vocab/unit/YD> }

?unit  qudt:conversionMultiplier ?multiplier .

}

This example of conversionMultipliers answers our second question; to convert values from one unit of measure to another unit of measure, first multiply by the conversionMultiplier of the “from” unit and then divide by the conversionMultiplier of the “to” unit. [note: for temperatures, offsets are also needed]

Question 3: How does QUDT support dimensional analysis?

To answer our third question we will start with a simple example:

Force = mass x acceleration

In the following query, we retrieve the exponents of Mass, Acceleration, and Force to validate that Force does indeed equal Mass x Acceleration:

prefix qudt: <http://qudt.org/schema/qudt/>

prefix rdf:  <http://www.w3.org/1999/02/22-rdf-syntax-ns#>

prefix rdfs: <http://www.w3.org/2000/01/rdf-schema#>

prefix owl:  <http://www.w3.org/2002/07/owl#>

prefix xsd:  <http://www.w3.org/2001/XMLSchema#>

select  ?qk ?dv ?exponentForMass ?exponentForLength ?exponentForTime

where {

values ?qk {

<http://qudt.org/vocab/quantitykind/Mass>

<http://qudt.org/vocab/quantitykind/Acceleration>

<http://qudt.org/vocab/quantitykind/Force> }

?qk  qudt:hasDimensionVector ?dv  .

?dv qudt:dimensionExponentForMass   ?exponentForMass  ;

qudt:dimensionExponentForLength ?exponentForLength ;

qudt:dimensionExponentForTime   ?exponentForTime ;

.

}

Recall that to multiply “like terms” with exponents, add the exponents, e.g.

length¹ x length² = length³

In the QUDT output, look at the columns for Mass, Length, and Time. Note that in each column the exponents associated with Mass and Acceleration add up to the exponent associated with Force, as expected.

Question 4: How can units be defined in terms of the International System of Units?

Finally, we want to see how QUDT can be used to define units in terms of the base units of the International System of Units as defined in the SI Brochure. We want to end up with equations like:

1 inch = 0.0254 meters

1 foot per second squared = 0.3048 meters per second squared

1 pound per cubic yard = 0.5932764212577829 kilograms per cubic meter

Delving deeper into QUDT, we see the concept of QuantityKindDimensionVector. Every unit and every quantity kind is related to one of these QuantityKindDimensionVectors.

Let’s unpack what that means by way of an example where we show the dimension vector A0E0L1I0M0H0T-2D0 means Length x Time^-2 (linear acceleration):

Start with dimension vector: A0E0L1I0M0H0T-2D0

Each letter stands for a base dimension, and the vector can also be written as:

Amount⁰ x ElectricCurrent⁰ x Length¹ x Intensity⁰ x Mass⁰ x Heat⁰ x Time^-2 x Other⁰

Every term with an exponent of zero equals 1, so this expression can be reduced to:

Length x Time^-2 (also known as Linear Acceleration)

The corresponding expression in terms of base units of the International System of Units is:

Meter x Second^-2 (the standard unit for acceleration)

… which can also be written as:

meter per second squared

Using this example as a pattern, we can proceed to query QUDT to get an equation for each QUDT unit in terms of base units. To reduce the size of the query we will focus on mechanics, where the base dimensions are Mass, Length, and Time and the corresponding base units are kilogram, meter, and second.

Here is the query to create the equations we want; run it on the QUDT SPARQL Endpoint and see what you get:

prefix qudt: <http://qudt.org/schema/qudt/>

prefix rdf: <http://www.w3.org/1999/02/22-rdf-syntax-ns#>

prefix rdfs: <http://www.w3.org/2000/01/rdf-schema#>

prefix owl: <http://www.w3.org/2002/07/owl#>

prefix xsd: <http://www.w3.org/2001/XMLSchema#>

select distinct ?equation

where {

?unit rdf:type  qudt:Unit ;

qudt:conversionMultiplier ?multiplier ;

qudt:hasDimensionVector ?dv ;

rdfs:label ?unitLabel ;

.

?dv qudt:dimensionExponentForMass    ?expKilogram ;  # translate to units

qudt:dimensionExponentForLength  ?expMeter ;

qudt:dimensionExponentForTime    ?expSecond ;

rdfs:label ?dvLabel ;

.

filter(regex(str(?dv), “A0E0L.*I0M.*H0T.*D0”)) # mechanics

filter(!regex(str(?dv), “A0E0L0I0M0H0T0D0”))

filter(?multiplier > 0)

bind(str(?unitLabel) as ?unitString)

# to form a label for the unit:

#    put positive terms first

#    omit zero-exponent terms

#    change exponents to words

bind(if(?expKilogram > 0, concat(“_kilogram_”, str(?expKilogram)), “”) as ?SiUnitTerm4)

bind(if(?expMeter    > 0, concat(“_meter_”,    str(?expMeter)),    “”) as ?SiUnitTerm5)

bind(if(?expSecond   > 0, concat(“_second_”,   str(?expSecond)),   “”) as ?SiUnitTerm7)

bind(if(?expKilogram < 0, concat(“_kilogram_”, str(-1 * ?expKilogram)), “”) as ?SiUnitTerm104)

bind(if(?expMeter    < 0, concat(“_meter_”,    str(-1 * ?expMeter)),    “”) as ?SiUnitTerm105)

bind(if(?expSecond   < 0, concat(“_second_”,   str(-1 * ?expSecond)),   “”) as ?SiUnitTerm107)

bind(concat(?SiUnitTerm4,   ?SiUnitTerm5,   ?SiUnitTerm7)   as ?part1)

bind(concat(?SiUnitTerm104, ?SiUnitTerm105, ?SiUnitTerm107) as ?part2)

bind(if(?part2 = “”, ?part1,

if(?part1 = “”, concat(“per”,?part2),

concat(?part1, “_per”, ?part2))) as ?SiUnitString1)

bind(replace(?SiUnitString1, “_1_|_1$”, “_”)             as ?SiUnitString2)

bind(replace(?SiUnitString2, “_2_|_2$”, “Squared_”)      as ?SiUnitString3)

bind(replace(?SiUnitString3, “_3_|_3$”, “Cubed_”)        as ?SiUnitString4)

bind(replace(?SiUnitString4, “_4_|_4$”, “ToTheFourth_”)  as ?SiUnitString5)

bind(replace(?SiUnitString5, “_5_|_5$”, “ToTheFifth_”)   as ?SiUnitString6)

bind(replace(?SiUnitString6, “_6_|_6$”, “ToTheSixth_”)   as ?SiUnitString7)

bind(replace(?SiUnitString7, “_7_|_7$”, “ToTheSeventh_”) as ?SiUnitString8)

bind(replace(?SiUnitString8, “_8_|_8$”, “ToTheEighth_”)  as ?SiUnitString9)

bind(replace(?SiUnitString9, “_9_|_9$”, “ToTheNinth_”)   as ?SiUnitString10)

bind(replace(?SiUnitString10, “_10_|_10$”,”ToTheTenth_”)  as ?SiUnitString11)

bind(replace(?SiUnitString11,  “^_”,  “”)  as ?SiUnitString12) # tidy up

bind(replace(?SiUnitString12,  “_$”,  “”)  as ?SiUnitString13)

bind(?SiUnitString13 as ?SiUnitLabel)

bind(concat(“1 “, str(?unitLabel), ” = “, str(?multiplier), ”  “,   ?SiUnitLabel) as ?equation)

}

order by ?equation

The result of this query is a set of equations that tie more than 1200 units back to the base units of the International System of Units, which in turn are defined in terms of seven fundamental physical constants.

And that’s a wrap. We answered all four questions with only 3 QUDT classes and 6 QUDT properties:

1. What units are applicable for a given measurable characteristic?
2. How do I convert a value from one unit to another?
3. How does QUDT support dimensional analysis?
4. How can units be defined in terms of the International System of Units?

For future reference, here’s a map of the territory we explored:

One final note: kudos to everyone who contributed to QUDT; it has a lot of great information in one place. Thank you!